Distribución estacionaria de una Cadena de Markov
Se dice que una Cadena de Markov en tiempo discreto admite una distribución estacionaria en la medida que las probabilidades de largo plazo existen y es independiente de la distribución inicial (f0).
En este sentido se deben verificar ciertos requisitos para la existencia de esta distribución de probabilidades de largo plazo: la cadena debe ser irreducible y sus estados deben ser recurrentes positivos aperiódicos. Se recomienda revisar en detalle la clasificación de estados antes del cálculo de la distribución estacionaria.
La distribución estacionaria se obtiene a través de la solución única del siguiente sistema de ecuaciones:
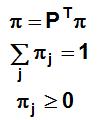
Ejemplo cálculo distribución estacionaria de una Cadena de Markov
Considere la siguiente matriz de transición de probabilidades para un proceso markoviano en tiempo discreto:

Calcule la probabilidad de encontrarse en cada uno de los estados en el largo plazo.
Desarrollo: Para verificar la existencia de una distribución estacionaria debemos analizar si la cadena es irreducible (es decir, existe una única clase de estados) y los estados que la componen son recurrentes positivos aperiódicos. Para facilitar este proceso se recomienda utilizar una representación gráfica o grafo:
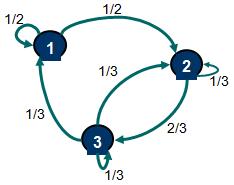
El estado 2 es accesible desde el estado 1, es decir, existe una probabilidad no nula que comenzando en el estado 1 se pueda llegar al estado 2 al cabo de n etapas (no necesariamente esto debe ser al cabo de una etapa). También se puede verificar que el estado 1 es accesible desde el estado 2, por tanto se concluye que el estado 1 y 2 se comunican. Cabe destacar que 2 estados que se comunican pertenecen a una misma clase de estados. Adicionalmente se puede demostrar que el estado 3 es accesible desde el estado 2 y el estado 2 es accesible desde el estado 3. Por tanto el estado 2 y 3 se comunican y por transitividad el estado 1 y 3 se comunican. Se concluye entonces que existe una sola clase de estados que contiene a {1,2,3} y por tanto la cadena es irreducible.
Los estados 1, 2 y 3 son recurrentes y dado que la cadena tiene una cantidad finita de estados se puede afirmar que éstos son recurrentes positivos.
Finalmente los estados son aperiódicos, es decir, no existe una secuencia de pasos tal para que comenzando en uno de ellos se pueda volver sobre si mismo (con probabilidad no nula) al cabo de un cierto número de pasos o etapas.
Una vez que se han verificado las condiciones necesarias para la existencia de una distribución estacionaria se formula el sistema de ecuaciones que permitirá encontrar las probabilidades de estado de largo plazo. En nuestro ejemplo el sistema queda definido por:
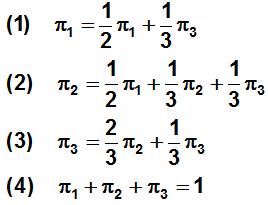
La resolución del sistema anterior permite encontrar que:
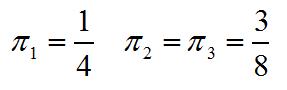
Se concluye que en el largo plazo la probabilidad de estar en el estado 1 es de un 25% y la probabilidad de estar en el estado 2 y 3 es de un 37,5%.