EOQ con descuentos por Cantidad
El modelo EOQ con descuentos por cantidad es una extensión del modelo básico de EOQ revisado en la sección anterior y mantiene sus supuestos. Se asume que el costo de adquisición (C) disminuye en la medida que aumenta el tamaño de lote. Adicionalmente se considera que el costo de almacenar una unidad en inventario es un porcentaje (I) del costo de adquisición. Por tanto la fórmula a utilizar es:
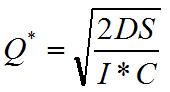
Al existir un descuento por cantidad o volumen de compra se genera un incentivo a pedir lotes de un mayor tamaño, sin embargo, esto a la vez incrementa el costo de mantener unidades en inventario. Por tanto se busca determinar la cantidad óptima a pedir para cada nivel o quiebre de precios, analizar si dicho tamaño de pedido es factible, ajustar el tamaño de lote si es necesario y finalmente comparar las distintas alternativas para ver cuál de ellas provee el menor Costo Total el cual está definido por la siguiente expresión:
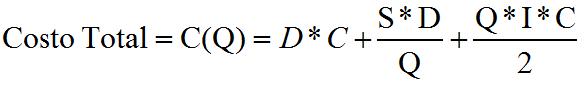
Ejemplo de EOQ con descuentos por cantidad
Un proveedor le ofrece la siguiente tabla de descuento para la adquisición de su principal producto, cuya demanda anual usted ha estimado en 5.000 unidades. El costo de emitir una orden de pedido es de $49 y adicionalmente se ha estimado que el costo anual de almacenar una unidad en inventario es un 20% del costo de adquisición del producto. ¿Cuál es la cantidad de la orden que minimiza el costo total del inventario?.
Tamaño del Lote (Unidades) |
Descuento (%) |
Valor del Producto ($/Unidad) |
0 a 999 |
0% |
5 |
1.000 a 1999 |
4% |
4,8 |
2.000 o más |
5% |
4,75 |
Para dar respuesta a esta situación se propone seguir los siguientes pasos:
PASO 1: Determinar el tamaño óptimo de pedido (Q*) para cada nivel o quiebre de precios.
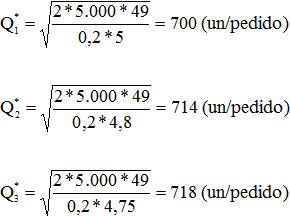
PASO 2: Ajustar la cantidad a pedir en cada quiebre de precio en caso de ser necesario. En nuestro ejemplo para el tramo 1 Q(1)=700 unidades esta en el intervalo por tanto se mantiene; para el tramo 2 Q(2)=714 está por debajo de la cota inferior del intervalo, por tanto se aproxima a esta cota quedando Q(2)=1.000; finalmente en el tramo 3 Q(3)=718 que también está por debajo de la cota inferior del intervalo, por tanto se aproxima a esta cota quedando Q(3)=2.000
PASO 3: Calcular el costo asociado a cada una de las cantidades determinadas (utilizando la fórmula de costo total presentada anteriormente)
Costo Tramo 1 = C(700)=$25.700
Costo Tramo 2 = C(1.000)=$24.725
Costo Tramo 3 = C(2.000)=$24.822
Se concluye que el tamaño óptimo de pedido que minimiza los costos totales es 1.000 unidades, con un costo total anual de $24.725.